前にpythonでやったことをOCamlでやったのでまとめた。
このページの実行例はこのリポジトリ のルートで jbuilder utop src で起動するutopで実行した。
作成・実行
作って…
# let dfa =
DFA . cons
[ "0" ; "1" ] (* アルファベット *)
[( 0 , "0" , 0 ); (* 遷移関数 *)
( 0 , "1" , 1 ); (* (q, c, q') は「状態qでcを読むとq'に遷移する」を意味する *)
( 1 , "0" , 0 );
( 1 , "1" , 1 )]
0 (* 初期状態 *)
[ 1 ];; (* 受理状態 *)
val dfa : int DFA . t = < abstr > 走らせる。
# DFA . run dfa "0001" ;;
- : bool = true
# DFA . run dfa "0110" ;;
- : bool = false
# DFA . run dfa "" ;;
- : bool = false NFAでは空文字列Emptyと「その他全て」を意味するAnyOtherが使える
# let nfa =
let a , b , c , d = 1 , 2 , 3 , 4 in
NFA . cons [ "0" ; "1" ; "2" ]
[( a , Char "0" , [ a ]); (* 遷移先は状態ではなく状態の集合になる *)
( a , AnyOther , [ b ]);
( b , Char "1" , [ b ]);
( b , AnyOther , [ c ]);
( c , Char "2" , [ c ]);
( c , Empty , [ a ; b ])]
[ a ] (* 初期状態も状態の集合*)
[ c ];;
val nfa : int NFA . t = < abstr >
# NFA . run nfa "" ;;
- : bool = false
# NFA . run nfa "00" ;;
- : bool = false
# NFA . run nfa "10" ;;
- : bool = true
# NFA . run maton "21012" ;;
- : bool = true
# NFA . run nfa "011010001" ;;
- : bool = false 遷移図の出力
Dot言語のソースコードを出力する関数がある。
# DFA . print_dfa dfa string_of_int ;;
digraph finite_state_machine {
rankdir = LR
node [ shape = point ] init
node [ shape = ellipse , peripheries = 2 ]
"1"
node [ shape = ellipse , peripheries = 1 ]
init -> "0"
node [ shape = ellipse , peripheries = 1 ]
"0" -> "0" [ label = "0" ]
"0" -> "1" [ label = "1" ]
"1" -> "0" [ label = "0" ]
"1" -> "1" [ label = "1" ]
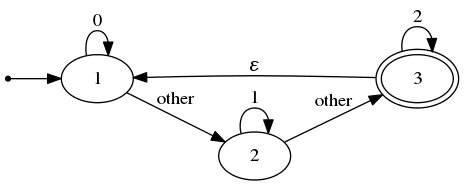
} これをgraphvizでコンパイルすると、以下の画像が得られる。
NFAでも同様。
# print_nfa nfa string_of_int ;;
digraph finite_state_machine {
rankdir = LR
node [ shape = point ] init
node [ shape = ellipse , peripheries = 2 ]
"3"
node [ shape = ellipse , peripheries = 1 ];
init -> "1"
node [ shape = ellipse , peripheries = 1 ]
"1" -> "1" [ label = "0" ]
"1" -> "2" [ label = "other" ]
"2" -> "2" [ label = "1" ]
"2" -> "3" [ label = "other" ]
"3" -> "3" [ label = "2" ]
"3" -> "1" [ label = "ε" ]
"3" -> "2" [ label = "ε" ]
}
NFAのDFAへの変換
与えられたNFAを、認識する言語が同じDFAに変換するアルゴリズムを実装した。
これだけ読んで分かるかどうかは微妙だが、ソースコードを張る。
let to_dfa = fun maton ->
let init = ( saturate maton maton . initial ) in
let finals =
if anything_in_common init maton . finals
then ref [ init ]
else ref [] in
let trans = ref [] in
let rec loop searched to_search =
match to_search with
| [] -> ()
| state :: tl ->
let nexts_triplet =
image ( fun c -> state , c , transit maton state c ) maton . alphabet in
let nexts = map ( fun (_, _, x ) -> x ) nexts_triplet in
trans := nexts_triplet @ ! trans ;
finals := nexts
|> filter ( anything_in_common maton . finals )
|> union ! finals ;
loop ( set_add searched state ) ( union tl ( diff nexts ( state :: searched )))
in
let _ = loop [] [ init ] in
DFA . cons maton . alphabet ! trans init ! finals 次のように使う。
# let nfa =
let a , b , c = 0 , 1 , 2 in
NFA . cons [ "0" ; "1" ; "2" ]
[( a , Char "0" , [ a ]);
( a , Empty , [ b ]);
( b , Char "1" , [ b ]);
( b , Empty , [ c ]);
( c , Char "2" , [ c ])]
[ a ] [ c ] ;;
val nfa : int NFA . t = < abstr >
# let dfa = ( NFA . to_dfa nfa );;
val dfa : int list DFA . t = < abstr > 変換されたDFAの状態は元のNFAの状態の集合なので、
int NFA.t を変換した dfa の型が int list DFA.t になっている。
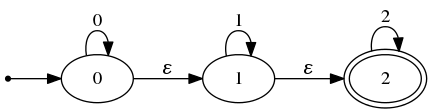
この nfa , dfa を画像にすると、変換がどう行われたのかが分かる。
# NFA . print_nfa nfa string_of_int ;;
(* 出力される文字列をgraphvizで画像にしたものを張った。以下同じ。 *)
# DFA . print_dfa dfa ( ListExt . string_of_list string_of_int )
DFAの最小化
Myhill–Nerodeの関係を使ったDFAの最小化アルゴリズムも実装した。
コードはかなり長く、以下のようになる。
let minimize maton =
(* helper functions *)
let transitable_into marked ( p , q ) =
exists
( fun c ->
let p' , q' = transit maton p c , transit maton q c in
mem ( p' , q' ) marked || mem ( q' , p' ) marked )
maton . alphabet in
let mark_initial_cond ( p , q ) =
( mem p maton . finals && not ( mem q maton . finals )) ||
( not ( mem p maton . finals ) && mem q maton . finals ) in
let transitions_from s new_states =
let origin = find ( mem s ) new_states
and next c = find ( mem ( transit maton s c )) new_states in
( map ( fun c -> origin , c , next c ) maton . alphabet ) in
let states = collect_states maton in
let rec loop ( marked , unmarked ) =
let to_add = filter ( transitable_into marked ) unmarked in
if subset to_add marked then marked , unmarked
else loop (( union marked to_add ), ( diff unmarked to_add )) in
let connected_component udgraph v =
let rec loop acc = function
| [] -> acc
| ( x , y ) :: tl when x = v || y = v -> loop ( union acc [ x ; y ]) tl
| _ :: tl -> loop acc tl in
loop [ v ] udgraph in
(* main procedure *)
(* (p, q) ∈ marked <-> p and q are distinguishable *)
let init_marked , init_unmarked =
partition mark_initial_cond ( original_pairs states ) in
(* saturate marked and unmarked *)
(* "marked ∩ unmarked = ∅" stays true after loop *)
let marked , unmarked = loop ( init_marked , init_unmarked ) in
(* calculate new states from marked and unmarked *)
let new_states =
fold_left_ignore
( fun acc s -> exists ( fun set -> mem s set ) acc )
(* largest undistinguishable set which contains s *)
( fun acc s -> ( connected_component unmarked s ) :: acc )
[] states in
(* also calculate new transition from new_states *)
let new_trans =
fold_left_ignore
( fun acc s -> exists ( fun ( set , _, _) -> mem s set ) acc )
( fun acc s -> ( transitions_from s new_states ) @ acc )
[] states in
cons
maton . alphabet
new_trans
(* note : exactly one element of new_states contains maton.inits *)
( find ( mem maton . inits ) new_states )
( filter ( anything_in_common maton . finals ) new_states ) 使用例:
# let maton = DFA . cons [ "0" ; "1" ]
[( 0 , "0" , 1 );
( 0 , "1" , 2 );
( 1 , "0" , 0 );
( 1 , "1" , 3 );
( 2 , "0" , 4 );
( 2 , "1" , 5 );
( 3 , "0" , 4 );
( 3 , "1" , 5 );
( 4 , "0" , 4 );
( 4 , "1" , 5 );
( 5 , "0" , 5 );
( 5 , "1" , 5 )]
0 [ 2 ; 3 ; 4 ] ;;
val maton : int DFA . t = < abstr >
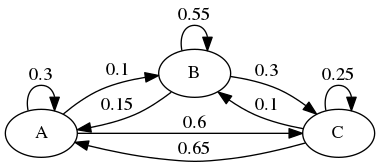
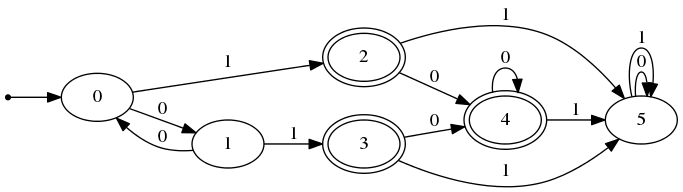
# DFA . print_dfa maton string_of_int ;;
これを最小化すると、
# let minimized = DFA . minimize maton ;;
val minimized : int list DFA . t = < abstr >
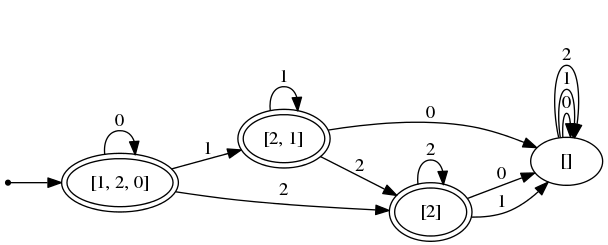
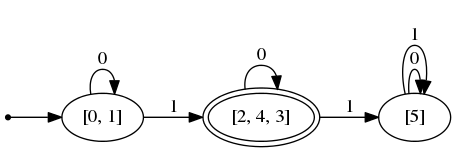
# DFA . print_dfa minimized ( MyExt . ListExt . string_of_list string_of_int );;
となる。
最小化されたDFAを見ると元のDFAのどの状態が同一視されているのかが分かる。
整数の組 \((i, j)\) に対してランダムな整数を割り振りたい。
それも、全ての組について乱数を保存することなく割り振りたい。
# モジュールのインポート
% matplotlib inline
from math import floor
from itertools import product
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
matplotlib . rcParams [ "figure.figsize" ] = ( 10 , 10 ) 失敗例
_random = np . random . permutation ( 256 )
def not_random_pick ( i , j ):
return _random [( i + j ) % 256 ] こうすると \(random\_pick(i, j) = random\_pick(i - 1, j + 1)\) が成り立ってしまうので値がランダムにならない。
canvas = np . array ([[ not_random_pick ( i , j ) for i in range ( 256 )] for j in range ( 256 )])
plt . imshow ( canvas / 256 , cmap = plt . cm . binary )
プロットすると全くランダムでないのがよく分かる。
成功例
\(random\_pick(i, j) = random\_pick(i - 1, j + 1)\) が成り立つのがまずいので、以下のように _random から値を二回取り出すようにすれば良い。
_random[x] と _random[x+1] には関連がないので、 random_pick(i, j) の返り値もランダムになる。
_random = np . random . permutation ( 256 )
def random_pick ( i , j ):
return _random [( _random [ i ] + j ) % 256 ] canvas = np . array ([[ random_pick ( i , j ) for i in range ( 256 )] for j in range ( 256 )])
plt . imshow ( canvas / 256 , cmap = plt . cm . binary )
工夫
mod演算無し
_random から値を取り出すときに (_random[i] + j) % 256 が配列の大きさを超えないようにモジュロ演算をしているが、
_random に入っている値 と j には制限があるので、 _random の長さを大きくすることでモジュロ演算を省くことができる。
_random = np . zeros ( 512 , dtype = np . int ) # 512 = (_random[x]の最大値) + (jの最大値)
for i , val in enumerate ( np . random . permutation ( 256 )):
_random [ i ] = val
_random [ i + 256 ] = val
def random_pick ( i , j ):
return _random [ _random [ i ] + j ]
canvas = np . array ([[ random_pick ( i , j ) for i in range ( 256 )] for j in range ( 256 )])
plt . imshow ( canvas / 256 , cmap = plt . cm . binary )
高次元化
高次元でも「 _random から引いてきた値に引数を足してまた _random から引く」を繰り返せば同じことができる。
_random = np . random . permutation ( 256 )
def random_pick_higher_order ( args ):
ans = 0
for x in args :
ans = _random [( ans + x ) % 256 ]
return ans
# 3次元でやる
canvas = np . array ([[[ random_pick_higher_order ([ i , j , k ]) for i in range ( 256 )]
for j in range ( 256 )] for k in range ( 256 )])
fig , ( ax0 , ax1 , ax2 ) = plt . subplots ( ncols = 3 , figsize = ( 10 , 30 ))
# 適当に切ってプロットする
ax0 . imshow ( canvas [:, :, 32 ] / 256 , cmap = plt . cm . binary )
ax1 . imshow ( canvas [:, 63 , :] / 256 , cmap = plt . cm . binary )
ax2 . imshow ( canvas [ 157 , :, :] / 256 , cmap = plt . cm . binary )
返り値を整数以外にする
random_picker の返り値を使って別の配列から引くようにすれば任意のオブジェクトを返すようにできる。
_alphabets = "abcdefghijklmnopqrstuvwxyz"
_random = np . random . permutation ( 26 )
def random_pick_alphabet ( i , j ):
return _alphabets [ _random [( _random [ i % 26 ] + j ) % 26 ]]
canvas = [[ random_pick_alphabet ( i , j ) for i in range ( 10 )] for j in range ( 10 )]
for xs in canvas :
for x in xs :
print ( x , end = " " )
print ( "" ) g j w s e f b p c t
m b t l u y e v a n
o e n w x q u c g h
j u h t k s x a m r
b x r n i l k g o d
e k d h z w i m j p
u i p r f t z o b v
x z v d y n f j e c
k f c p q h y b u a
i y a v s r q e x gまとめ
クラスにまとめる。
このクラスはコンストラクタの引数として配列を受け取り、
インスタンスに関数呼び出しをするとその配列の要素がランダムに返る。
class RandomPicker ():
# とりあえず256としておいて、必要ならば後で更新する
# 256のままだと picker(10, 0) = picker(266, 256) となる
random_size = 256
random = np . random . permutation ( random_size )
def __init__ ( self , base , arg_max = 0 ):
# arg_maxには予想される引数の最大値を渡す
# 予想できない/ランダム性がそれほど必要ない 場合はデフォルトのままでいい
self . base = base
arg_max = max ( len ( base ), arg_max )
if arg_max > RandomPicker . random_size :
RandomPicker . random_size = arg_max
RandomPicker . random = np . random . permutation ( arg_max )
def __call__ ( self , * args ):
ans = RandomPicker . random [ args [ 0 ] % RandomPicker . random_size ]
for i in range ( 1 , len ( args )):
ans = RandomPicker . random [( ans + args [ i ]) % RandomPicker . random_size ]
return self . base [ ans % len ( self . base )] 次のように使う。
picker = RandomPicker ( np . linspace ( 0.0 , 1.0 , 10 ))
canvas = np . array ([[( picker ( i - 1 , j - 1 ))
for i in range ( 256 )]
for j in range ( 256 )])
plt . imshow ( canvas , cmap = plt . cm . binary )
要素数\(10+256=266\) の配列を確保するだけで\(256\times256\)のホワイトノイズを作れて嬉しい。
各ピクセルに対する処理(関数を適用する、隣接ピクセルの平均を取る…)が増えればそれだけこの方法による利点は大きくなる。